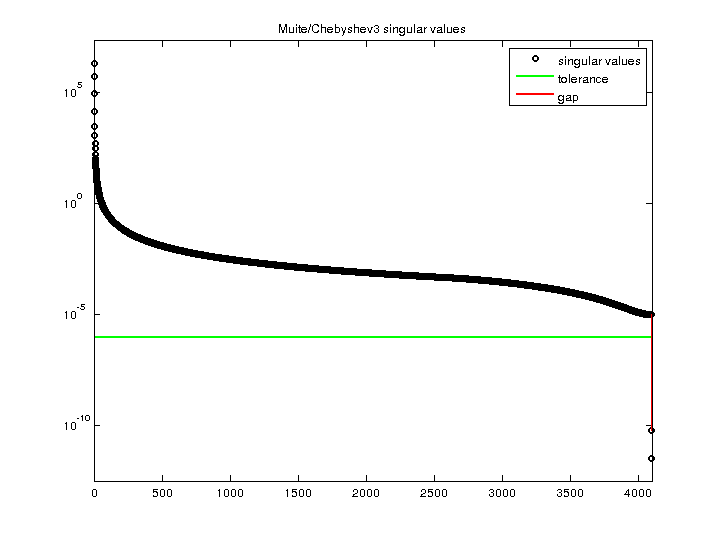
Muite/Chebyshev3
Integration matrix, Chebyshev method, 4th order semilinear initial BVP
| Name |
Chebyshev3 |
| Group |
Muite |
| Matrix ID |
1866 |
|
Num Rows
|
4,101 |
|
Num Cols
|
4,101 |
|
Nonzeros
|
36,879 |
|
Pattern Entries
|
36,879 |
|
Kind
|
Structural Problem |
|
Symmetric
|
No |
|
Date
|
2007 |
|
Author
|
B. Muite |
|
Editor
|
T. Davis |
| Structural Rank |
4,101 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
50% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
2.017564e+06 |
| Minimum Singular Value |
3.337566e-12 |
| Condition Number |
6.045017e+17
|
| Rank |
4,099 |
| sprank(A)-rank(A) |
2 |
| Null Space Dimension |
2 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Chebyshev integration matrix from Benson Muite, Oxford. Details of the
matrices can be found in a preprint at http://www.maths.ox.ac.uk/~muite
entitled "A comparison of Chebyshev methods for solving fourth-order
semilinear initial boundary value problems," June 2007. These matrices
are very ill-conditioned, partly because of the dense rows which are hard
to scale when coupled with the rest of the matrix.
|