About

The SuiteSparse Matrix Collection (formerly known as the University of Florida Sparse Matrix Collection), is a large and actively growing set of sparse matrices that arise in real applications. The Collection is widely used by the numerical linear algebra community for the development and performance evaluation of sparse matrix algorithms. It allows for robust and repeatable experiments: robust because performance results with artificially-generated matrices can be misleading, and repeatable because matrices are curated and made publicly available in many formats.

The matrices in the Collection cover a wide spectrum of domains, including

  • 2D or 3D Geometric Domains
    • Structural engineering
    • Computational fluid dynamics
    • Model reduction
    • Electromagnetics
    • Semiconductor devices
    • Thermodynamics
    • Material science
    • Acoustics
    • Computer graphics and vision
    • Robotics and kinematics
    • Other spatial discretizations

  • Non-Geometric Domains
    • Optimization
    • Economic and financial modeling
    • Circuit simulation
    • Theoretical and quantum chemistry
    • Chemical process simulation
    • Mathematics and statistics
    • Power networks
    • Other networks and graph-structured data

In addition to the matrices and associated metadata, we provide software for accessing the Collection via a number of interfaces, from MATLAB, Mathematica, Fortran, and C, as well as this web application and index.

Graph visualization of the matrices is provided on this site via graphviz.

The Collection is maintained by Tim Davis, Texas A&M University (email: davis@tamu.edu), Yifan Hu, Yahoo! Labs, and Scott Kolodziej.

General-audience description

Click here for an easy-to-understand description of the SuiteSparse Matrix Collection and its images. The page includes a video of a talk I gave at the Harn Museum at the University of Florida, for general audiences.

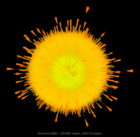
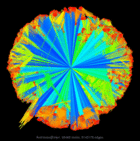
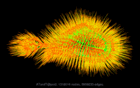
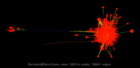
Sample Gallery of the SuiteSparse Matrix Collection:


Click on an image above for more details on each matrix. The images were created by Yifan Hu at Yahoo! Labs, with a graph drawing program that can generate truly beautiful drawings large graphs, based solely on the connectivity (that is, a sparse matrix). Take a look at his drawings of the matrices in the Collection, which are also mirrored here on the web page for each matrix.

How to Cite

Here are some citation recommendations when the Collection or this web interface are used as part of academic research:

Related Publications

For additional background and information about subsets of the Collection:

Archival data for reproducible research

The Collection serves a vital role in the sparse matrix algorithms community, as a benchmark for algorithmic testing and development. Results in journal articles that use these matrices can be repeated by other researchers. The Collection also appears widely in other repositories or citation indices:

To access the Collection

There are several ways to download matrices from this Collection.

See the Interfaces tab at the top of this page for details on ssget, the Java GUI, and the Julia interface. Matrices are provided in three formats: MATLAB *.mat file, Rutherford-Boeing, and Matrix Market. The Rutherford-Boeing format is described in a document on the Rutherford-Boeing Sparse Matrix Collection. See the Matrix Market for a description of the Matrix Market format.

To submit matrices to the Collection:

Click on the Submit Matrix tab in the top menu bar on this page to submit matrices to the Collection.

Other Computed Data

While the Collection contains a variety of precomputed data about each matrix, others have gone further and computed even more interesting properties for matrices from the Collection (or subset thereof). Here are a few:

You can submit more metrics, properties, or other work based off of the Collection to Tim Davis at davis@tamu.edu.

License

Overview

This website software (except for ssget) is under the MIT License. The matrices themselves are under the CC-BY 4.0 License.

Details

ssget (available in SuiteSparse/ssget in the ssget folder is under the BSD 3-clause License.

The matrices themselves are under the CC-BY 4.0 license Note that this license asks you to cite the source of the matrices. That citation can be made to these references:

You should also preserve the metadata in the matrices themselves, which includes additional citations for specific matrices. For example, the LAW set of matrices (from the Laboratory for Web Algorithmics, Universita degli Studi di Milano) includes specific instructions on how to properly cite the matrices. See sparse.tamu.edu/LAW for details. For the Matrix Market format, most of the metadata appears in the header of the *.mtx themselves.

Ideally, if you redistribute the matrices in your own applications, you should not change them at all. This is essential for repeatability of experiments that rely on these matrices. Modification is permitted under the CC-BY 4.0 License, but that license requires you to state the modifications you make. If you make any such modifications, please change the filename and matrix name to indicate that it differs from the copy of the matrix from sparse.tamu.edu. Carefully describe any modifications you make.