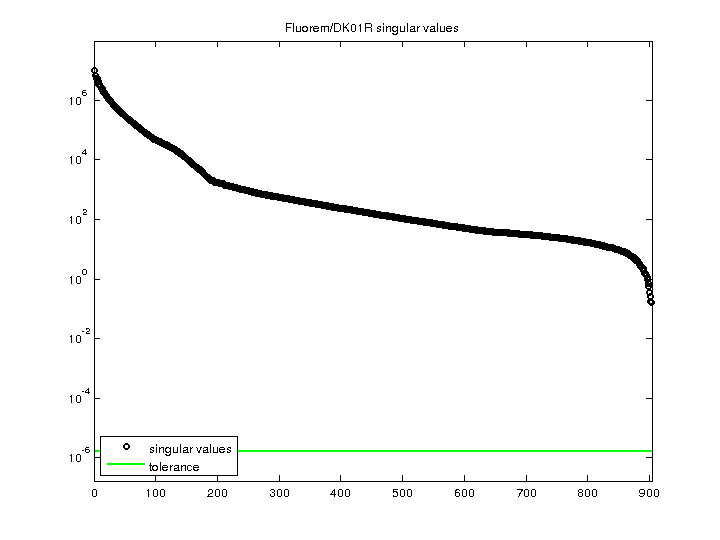
Fluorem/DK01R
DK01R: 1D turbulent case. F. Pacull, Lyon, France
| Name |
DK01R |
| Group |
Fluorem |
| Matrix ID |
2334 |
|
Num Rows
|
903 |
|
Num Cols
|
903 |
|
Nonzeros
|
11,766 |
|
Pattern Entries
|
11,766 |
|
Kind
|
Computational Fluid Dynamics Problem |
|
Symmetric
|
No |
|
Date
|
2010 |
|
Author
|
F. Pacull |
|
Editor
|
T. Davis |
| Structural Rank |
903 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
8 |
|
Strongly Connect Components
|
8 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
96.1% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
9.775521e+06 |
| Minimum Singular Value |
1.660209e-01 |
| Condition Number |
5.888126e+07
|
| Rank |
903 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
CFD matrices from Francois Pacull, FLUOREM, in Lyon, France
We are dealing with CFD and more precisely steady flow
parametrization. The equations involved are the compressible
Navier-Stokes ones (RANS). These matrices are real, square and
indefinite, they correspond to the Jacobian with respect the
conservative fluid variables of the discretized governing
equations (finite-volume discretization). Thus they have a
block structure (corresponding to the mesh nodes: the block
size is the number of variables per mesh node), they are not
symmetric (however, their blockwise structure has a high level
of symmetry) and they often show some kind of hyperbolic
behavior. They have not been scaled or reordered.
They are generated through automatic differentiation of the
flow solver around a steady state. A right hand-side is also
given for each matrix: this represents the derivative of the
equations with respect to a parameter (of operation or shape).
Since they are generated automatically, they may have "silent"
variables: these are variables corresponding to an identity
submatrix associated with a null right hand-side, for example
one of the three velocity components in a 2D case, or the
turbulent variables in a "frozen" turbulence case.
We believe that these matrices are good test cases when
studying preconditioning methods for iterative methods, such as
block incomplete factorization, or when studying domain
decomposition methods or deflation. They are actually being
studied by a few researchers in France regarding numerical
methods, through the LIBRAERO research project of the ANR (national
research agency): ANR-07-TLOG-011.
Francois Pacull, Lyon, France. fpacull at fluorem.com
Specific problem descriptions:
DK01R: 1D turbulent case
number of mesh nodes: 129
block size: 7
variables: [rho,rho*u,rho*v,rho*w,rho*E,rho*k,rho*omega]
(rho v and rho w are "silent", the third and fourth rows
and columns
in each block can be removed)
matrix order: 903
nnz: 11758
comments: The DK01R matrix corresponds to a small 1D turbulent
case. The grid has 129 nodes, non-uniformly spaced
(geometrical distribution). The number of unknowns per node is
7, leading to a linear system of 903 real algebraic equations.
The 1D discretization of the partial differential equations
uses a 5 points stencil, leading to a block penta-diagonal
matrix, each block having size 7 by 7. Each diagonal block is
related to two up- and two down-stream neighboring nodes,
corresponding respectively to the 14 upper and 14 lower matrix
rows, the node ordering being coherent with the 1D spatial
node distribution. The stationary flow on which the matrix is
based on is dominated by advection, characterized by a Mach
number around 0.3.
|