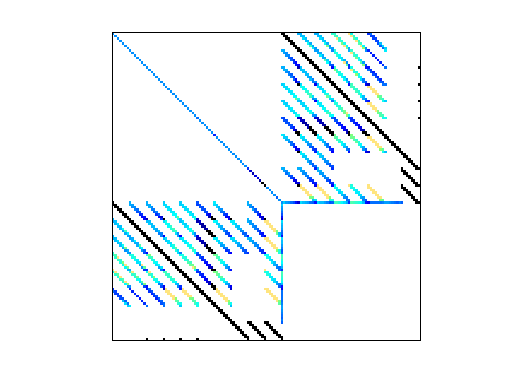
VDOL/lowThrust_12
lowThrust optimal control problem (matrix 12 of 13)
| Name |
lowThrust_12 |
| Group |
VDOL |
| Matrix ID |
2716 |
|
Num Rows
|
18,458 |
|
Num Cols
|
18,458 |
|
Nonzeros
|
224,593 |
|
Pattern Entries
|
224,593 |
|
Kind
|
Optimal Control Problem |
|
Symmetric
|
Yes |
|
Date
|
2015 |
|
Author
|
B. Senses, A. Rao |
|
Editor
|
T. Davis |
| Structural Rank |
18,458 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
100% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Optimal control problem, Vehicle Dynamics & Optimization Lab, UF
Anil Rao and Begum Senses, University of Florida
http://vdol.mae.ufl.edu
This matrix arises from an optimal control problem described below.
Each optimal control problem gives rise to a sequence of matrices of
different sizes when they are being solved inside GPOPS, an optimal
control solver created by Anil Rao, Begum Senses, and others at in VDOL
lab at the University of Florida. This is one of the matrices in one
of these problems. The matrix is symmetric indefinite.
Rao, Senses, and Davis have created a graph coarsening strategy
that matches pairs of nodes. The mapping is given for this matrix,
where map(i)=k means that node i in the original graph is mapped to
node k in the smaller graph. map(i)=map(j)=k means that both nodes
i and j are mapped to the same node k, and thus nodes i and j have
been merged.
This matrix consists of a set of nodes (rows/columns) and the
names of these rows/cols are given
Anil Rao, Begum Sense, and Tim Davis, 2015.
VDOL/lowThrust
Low-thrust orbit transfer optimal control problem is taken from
Ref.~\cite{betts2010practical}. The goal of the low-thrust orbit
transfer problem is to determine the state and the control that
minimize the fuel consumption during the orbit transfer of a
spacecraft that starts from a low-earth orbit and terminates at the
geostationary orbit via low-thrust propulsion systems. The highly
nonlinear dynamics of the low-thrust orbit transfer problem is given
in modified equinoctial elements (state of the system) and the thrust
direction (control of the system). Furthermore, the low-thrust
optimal control problem is a badly scaled problem because of the
small thrust-to-initial-mass ratio, that is typically on the order of
$O(10^{-4})$, and the long orbit transfer duration. Badly scaling of
the problem leads to a lot of delayed pivots. The specified accuracy
tolerance of $10^{-8}$ were satisfied after thirteen mesh iterations.
As the mesh refinement proceeds, the size of the KKT matrices
increases from 584 to 18476.
@book{betts2010practical,
title={Practical Methods for Optimal Control and Estimation Using
Nonlinear Programming},
author={Betts, John T},
volume={19},
year={2010},
publisher={SIAM Press},
address = {Philadelphia, Pennsylvania},
}
|