SNAP/ca-HepPh
Collaboration network of Arxiv High Energy Physics
| Name |
ca-HepPh |
| Group |
SNAP |
| Matrix ID |
2298 |
|
Num Rows
|
12,008 |
|
Num Cols
|
12,008 |
|
Nonzeros
|
237,010 |
|
Pattern Entries
|
237,010 |
|
Kind
|
Undirected Graph |
|
Symmetric
|
Yes |
|
Date
|
2003 |
|
Author
|
J. Leskovec, J. Kleinberg and C. Faloutsos |
|
Editor
|
J. Leskovec |
| Structural Rank |
|
| Structural Rank Full |
|
|
Num Dmperm Blocks
|
|
|
Strongly Connect Components
|
278 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
100% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
binary |
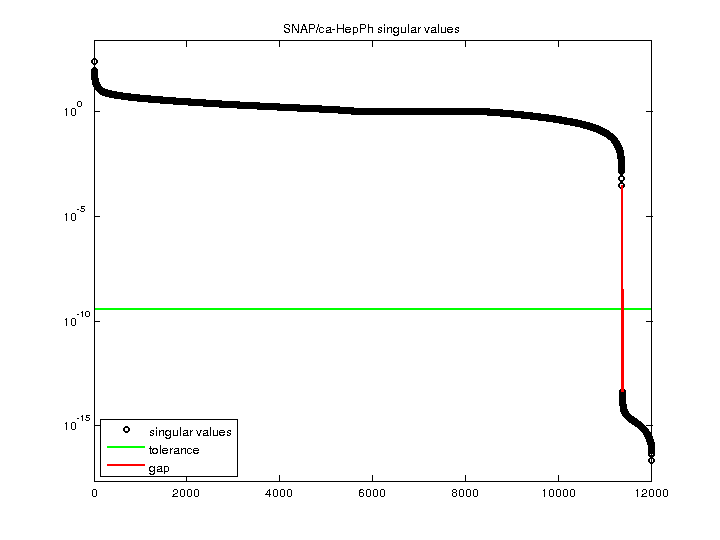
| SVD Statistics |
| Matrix Norm |
2.449394e+02 |
| Minimum Singular Value |
0 |
| Condition Number |
Inf
|
| Rank |
11,363 |
| sprank(A)-rank(A) |
|
| Null Space Dimension |
645 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Networks from SNAP (Stanford Network Analysis Platform) Network Data Sets,
Jure Leskovec http://snap.stanford.edu/data/index.html
email jure at cs.stanford.edu
High Energy Physics - Phenomenology collaboration network
Dataset information
Arxiv HEP-PH (High Energy Physics - Phenomenology) collaboration network is
from the e-print arXiv and covers scientific collaborations between authors
papers submitted to High Energy Physics - Phenomenology category. If an author
i co-authored a paper with author j, the graph contains a undirected edge from
i to j. If the paper is co-authored by k authors this generates a completely
connected (sub)graph on k nodes.
The data covers papers in the period from January 1993 to April 2003 (124
months). It begins within a few months of the inception of the arXiv, and thus
represents essentially the complete history of its HEP-PH section.
Dataset statistics
Nodes 12008
Edges 237010
Nodes in largest WCC 11204 (0.933)
Edges in largest WCC 235268 (0.993)
Nodes in largest SCC 11204 (0.933)
Edges in largest SCC 235268 (0.993)
Average clustering coefficient 0.6115
Number of triangles 3358499
Fraction of closed triangles 0.6595
Diameter (longest shortest path) 13
90-percentile effective diameter 5.8
Source (citation)
J. Leskovec, J. Kleinberg and C. Faloutsos. Graph Evolution: Densification and
Shrinking Diameters. ACM Transactions on Knowledge Discovery from Data (ACM
TKDD), 1(1), 2007.
Files
File Description
ca-HepPh.txt.gz Collaboration network of Arxiv High Energy Physics category
|