QY/case9
Transient stabilty constrained interior pt. optimal power flow, J. Quanyuan
| Name |
case9 |
| Group |
QY |
| Matrix ID |
2214 |
|
Num Rows
|
14,454 |
|
Num Cols
|
14,454 |
|
Nonzeros
|
147,972 |
|
Pattern Entries
|
147,972 |
|
Kind
|
Power Network Problem Sequence |
|
Symmetric
|
Yes |
|
Date
|
2008 |
|
Author
|
J. Quanyuan |
|
Editor
|
T. Davis |
| Structural Rank |
14,454 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
2 |
|
Strongly Connect Components
|
2 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
100% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
5.306192e+03 |
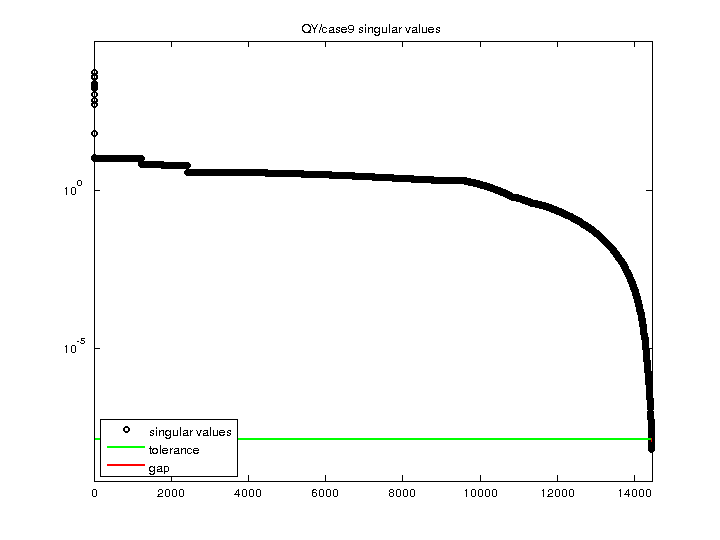
| Minimum Singular Value |
6.374288e-09 |
| Condition Number |
8.324369e+11
|
| Rank |
14,444 |
| sprank(A)-rank(A) |
10 |
| Null Space Dimension |
10 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Transient stabilty constrained interior pt. optimal power flow, J. Quanyuan
Two problem sets from Dr. Jiang Quanyuan from Zhejiang University,
Hangzhou, China, March, 2008, used in an electrical power system.
Each matrix A is solved sequentially with two right-hand-sides, b1 and
b2, one at a time. In the UF collection, the sequence of all first
and second right-hand-sides is in Problem.aux.b2 and Problem.aux.b1.
These matrices are symmetric indefinite (x=A\b uses MA57)
Note that the last matrices in the sequence are ill-conditioned.
Transient Stability Constrained Interior Point Optimal Power Flow Program
Version 1.0 -- Developed by Dr. Jiang Quanyuan, March 2008
case9.m - TSOPF converges after 12 iterations
object = 3.945939E+03
max_equ = 3.287326E-11
low_inequ = None
up_inequ = None
|