Pajek/Wordnet3
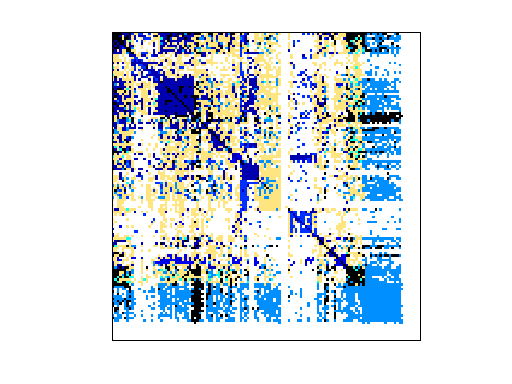
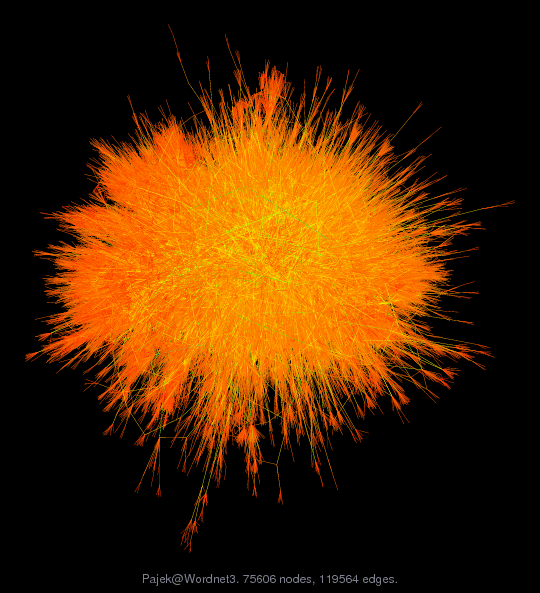
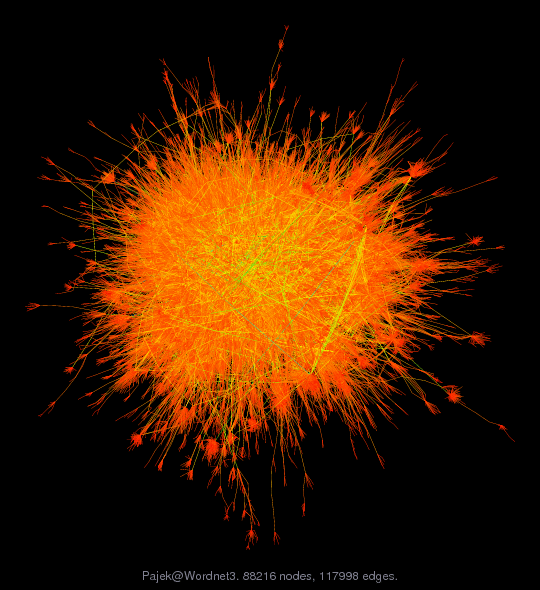
Pajek network: Wordnet3 dictionary network
| Name |
Wordnet3 |
| Group |
Pajek |
| Matrix ID |
1531 |
|
Num Rows
|
82,670 |
|
Num Cols
|
82,670 |
|
Nonzeros
|
132,964 |
|
Pattern Entries
|
132,964 |
|
Kind
|
Directed Weighted Graph |
|
Symmetric
|
No |
|
Date
|
2006 |
|
Author
|
|
|
Editor
|
V. Batagelj |
| Structural Rank |
|
| Structural Rank Full |
|
|
Num Dmperm Blocks
|
|
|
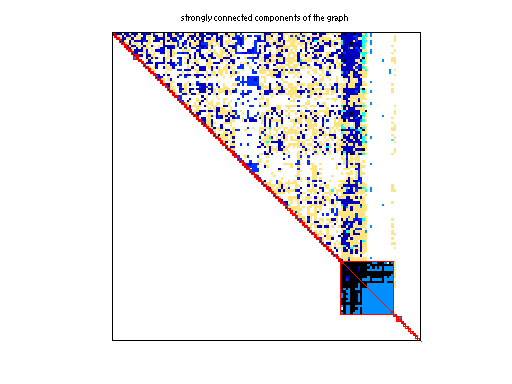
Strongly Connect Components
|
67,689 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
17.7% |
|
Numeric Symmetry
|
17.4% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
------------------------------------------------------------------------------
Pajek network converted to sparse adjacency matrix for inclusion in UF sparse
matrix collection, Tim Davis. For Pajek datasets, See V. Batagelj & A. Mrvar,
http://vlado.fmf.uni-lj.si/pub/networks/data/.
------------------------------------------------------------------------------
NOTE: this is a binary graph in the Pajek dataset, but where each edge has a
label (not a weight) in the range 1 to 9. The following labels are used:
1 hypernym pointer
2 entailment pointer
3 similar pointer
4 member meronym pointer
5 substance meronym pointer
6 part meronym pointer
7 cause pointer
8 grouped pointer
9 attribute pointer
This is not a multigraph. There are no edges (i,j) between the same nodes
with the same label. Thus, in the sparse matrix, the edge weight A(i,j)
represents the label 1 through 9 of edge (i,j). No loss of information
occurs in this translation. The above table is in aux.edgecode(1:9,:).
Each node is a word in a dictionary. aux.category(i) gives the category
of the word:
1: n (noun?) 63099 words
3: a (adjective?) 5501 words
4: r (?) 2846 words
5: s (?) 6728 words.
------------------------------------------------------------------------------
|