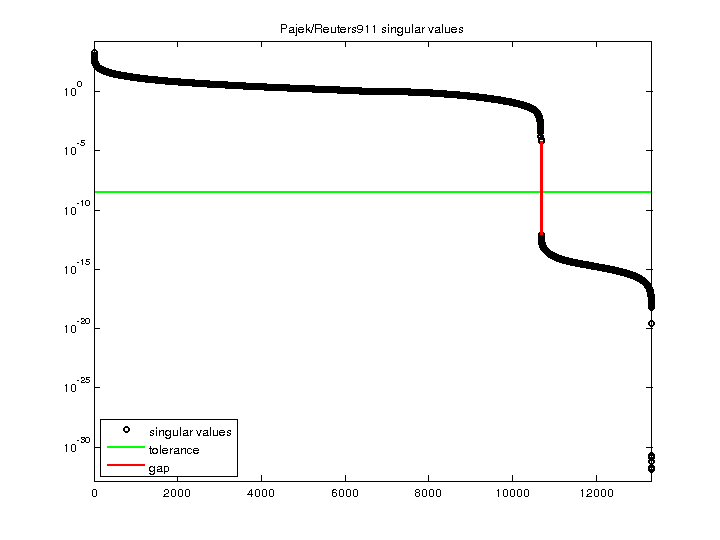
Pajek/Reuters911
Pajek network: Reuters news, Sept 11 to Nov 15, 2001
| Name |
Reuters911 |
| Group |
Pajek |
| Matrix ID |
1517 |
|
Num Rows
|
13,332 |
|
Num Cols
|
13,332 |
|
Nonzeros
|
296,076 |
|
Pattern Entries
|
296,076 |
|
Kind
|
Undirected Weighted Graph Sequence |
|
Symmetric
|
Yes |
|
Date
|
2001 |
|
Author
|
S. Corman, T. Kuhn, R. Mcphee, K. Dooley |
|
Editor
|
V. Batagelj, A. Mrvar |
| Structural Rank |
|
| Structural Rank Full |
|
|
Num Dmperm Blocks
|
|
|
Strongly Connect Components
|
22 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
100% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
| SVD Statistics |
| Matrix Norm |
1.904122e+03 |
| Minimum Singular Value |
1.372014e-32 |
| Condition Number |
1.387829e+35
|
| Rank |
10,682 |
| sprank(A)-rank(A) |
|
| Null Space Dimension |
2,650 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
------------------------------------------------------------------------------
Pajek network converted to sparse adjacency matrix for inclusion in UF sparse
matrix collection, Tim Davis. For Pajek datasets, See V. Batagelj & A. Mrvar,
http://vlado.fmf.uni-lj.si/pub/networks/data/. This is the "Days" network.
------------------------------------------------------------------------------
The Reuters terror news network is based on all stories released during 66
consecutive days by the news agency Reuters concerning the September 11 attack
on the U.S., beginning at 9:00 AM EST 9/11/01. The vertices of a network are
words (terms); there is an edge between two words iff they appear in the same
text unit (sentence). The weight of an edge is its frequency. The network has
n=13332 vertices (different words in the news) and m = 243447 edges, 50859
with value larger than 1. There are no loops in the network.
Steven R. Corman, Timothy Kuhn, Robert D. Mcphee and Kevin J. Dooley
(2002): Studying Complex Discursive Systems: Centering Resonance Analysis of
Communication.
------------------------------------------------------------------------------
When converted to a sparse adjacency matrix for the UF Sparse Matrix
Collection, Day{i} is the graph of the ith day. The diagonal entry
Day{i}(k,k) is 1 if word k appears in any news on the ith day. Note
that it may not appear in conjunction with other words in the same
sentence on that day. The sum of nnz(tril(Day{i})) for i=1:66 is 243,447.
The overall matrix A is the sum of the Day{i} matrices. A(i,j) is the number
of times words i and j appear in same sentence (for i not equal to j). A(k,k)
is the number of days the word k appears in any news report.
Note that this network has been renamed to Reuters911 here.
------------------------------------------------------------------------------
|