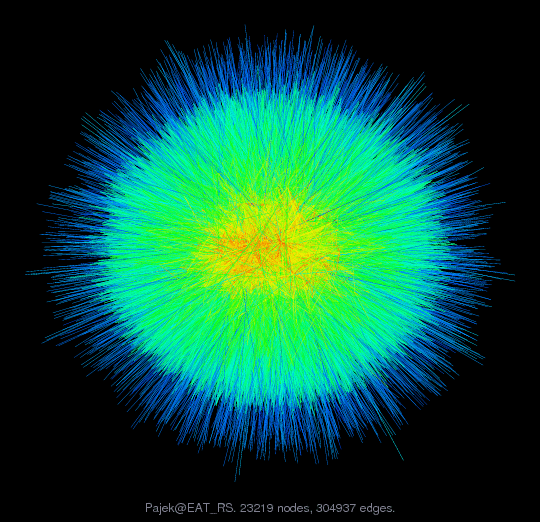
Pajek/EAT_RS
Pajek network: Edinburgh Associative Thesaurus (response-stimulus)
| Name |
EAT_RS |
| Group |
Pajek |
| Matrix ID |
1461 |
|
Num Rows
|
23,219 |
|
Num Cols
|
23,219 |
|
Nonzeros
|
325,592 |
|
Pattern Entries
|
325,592 |
|
Kind
|
Directed Weighted Graph |
|
Symmetric
|
No |
|
Date
|
1971 |
|
Author
|
G. Kiss, C. Armstrong R. Milroy, J. Piper |
|
Editor
|
V. Batagelj |
| Structural Rank |
|
| Structural Rank Full |
|
|
Num Dmperm Blocks
|
|
|
Strongly Connect Components
|
15,466 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
12.4% |
|
Numeric Symmetry
|
3.1% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
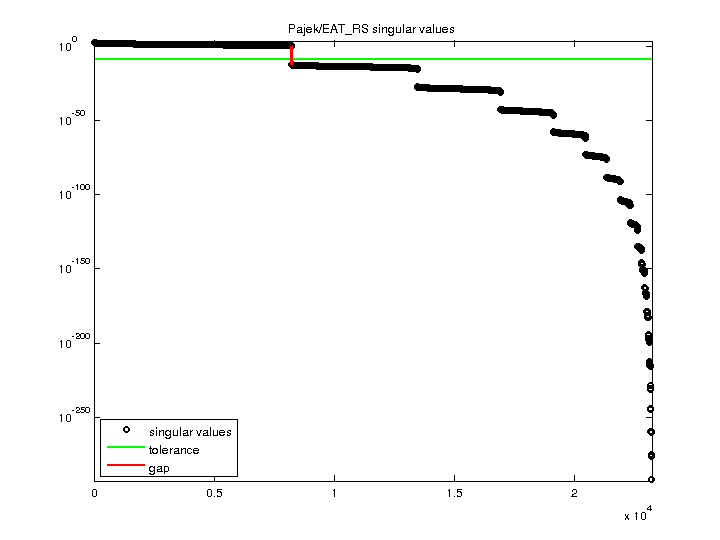
| SVD Statistics |
| Matrix Norm |
3.124415e+02 |
| Minimum Singular Value |
0 |
| Condition Number |
Inf
|
| Rank |
8,210 |
| sprank(A)-rank(A) |
|
| Null Space Dimension |
15,009 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
------------------------------------------------------------------------------
Pajek network converted to sparse adjacency matrix for inclusion in UF sparse
matrix collection, Tim Davis. For Pajek datasets, See V. Batagelj & A. Mrvar,
http://vlado.fmf.uni-lj.si/pub/networks/data/.
------------------------------------------------------------------------------
EAT - The Edinburgh Associative Thesaurus /
response-stimulus
--------------------------------------------------------
The EAT is a database of word association norms.
- Original EAT: George Kiss, Christine Armstrong,
Robert Milroy and J.R.I. Piper (1968-1971).
- MRC Psycholinguistic Database Version modified by:
Max Coltheart, S. James, J. Ramshaw, B.M. Philip,
B. Reid, J. Benyon-Tinker and E. Doctor;
made available by: Philip Quinlan.
- The present version was re-structured and documented
by Michael Wilson at the Rutherford Appleton Laboratory.
http://monkey.cis.rl.ac.uk/Eat/htdocs/eat.zip
transformed in Pajek format: V. Batagelj, 31. July 2003
-----
------------------------------------------------------------------------------
Regarding conversion for UF sparse matrix collection: in the original data
there are 325,624 weighted edges. Of those only 32 edges are duplicates, and
all of them have identical edge weights as the edges they are duplicates of
These extraneous edges have been removed, since this this appears to be a
graph, not a multigraph.
------------------------------------------------------------------------------
|