Mittelmann/nug08-3rd
LP lower bounds for quadratic assignment problems
| Name |
nug08-3rd |
| Group |
Mittelmann |
| Matrix ID |
1645 |
|
Num Rows
|
19,728 |
|
Num Cols
|
29,856 |
|
Nonzeros
|
148,416 |
|
Pattern Entries
|
148,416 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
1995 |
|
Author
|
S. Karisch, F. Rendl |
|
Editor
|
H. Mittelmann |
| Structural Rank |
19,728 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
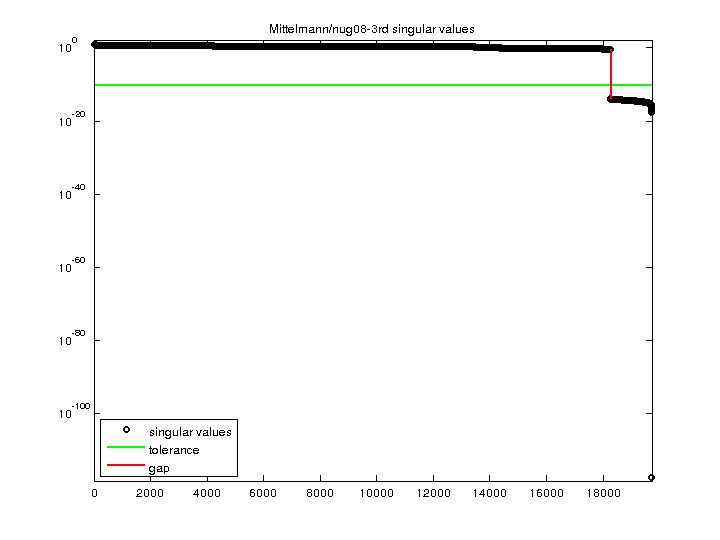
| SVD Statistics |
| Matrix Norm |
8.115185e+00 |
| Minimum Singular Value |
4.761293e-118 |
| Condition Number |
1.704408e+118
|
| Rank |
18,270 |
| sprank(A)-rank(A) |
1,458 |
| Null Space Dimension |
1,458 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Hans Mittelmann test set, http://plato.asu.edu/ftp/lptestset
minimize c'*x, subject to A*x=b and lo <= x <= hi
NUG: computing LP lower bounds for quadratic assignment problems. see
S.E. KARISCH and F. RENDL. Lower bounds for the quadratic assignment
problem via triangle decompositions. Mathematical Programming,
71(2):137-152, 1995.
K.G. Ramakrishnan, M.G.C. Resende, B. Ramachandran, and J.F. Pekny,
"Tight QAP bounds via linear programming," Combinatorial and Global
Optimization, P.M. Pardalos, A. Migdalas, and R.E. Burkard, eds.,
World Scientific Publishing Co., Singapore, pp. 297-303, 2002.
|