MathWorks/QRpivot
Limitation of basic solution to x=A\b using qr(A); needs min 2-norm
| Name |
QRpivot |
| Group |
MathWorks |
| Matrix ID |
1894 |
|
Num Rows
|
660 |
|
Num Cols
|
749 |
|
Nonzeros
|
3,808 |
|
Pattern Entries
|
3,808 |
|
Kind
|
Counter Example Problem |
|
Symmetric
|
No |
|
Date
|
2008 |
|
Author
|
P. Quillen |
|
Editor
|
T. Davis |
| Structural Rank |
660 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
9 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
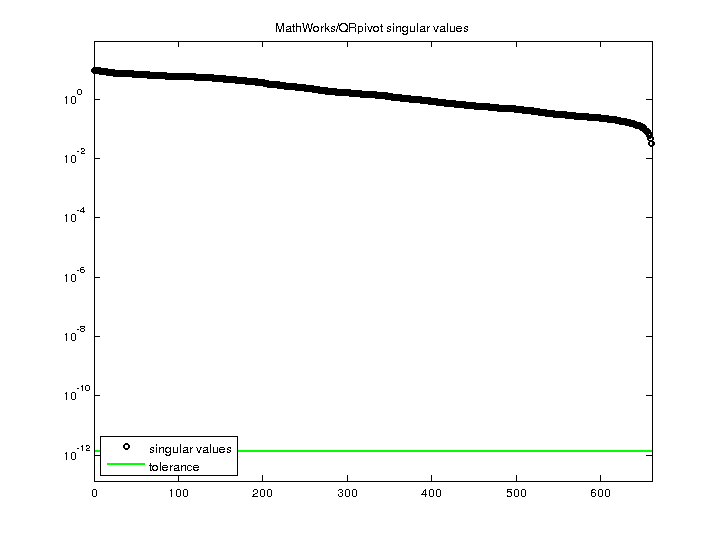
| Matrix Norm |
9.332323e+00 |
| Minimum Singular Value |
3.205865e-02 |
| Condition Number |
2.911016e+02
|
| Rank |
660 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Counter-example problem from The MathWorks, Pat Quillen
This matrix was obtained from a MATLAB user. It illustrates the
limitations inherent in computing a basic solution to an under-
determined system without the use of column pivoting.
With column pivoting (which can only be done in MATLAB with full
matrices) the problem is solved properly.
When finding the min 2-norm solution (ignoring fill-in):
[Q,R] = qr (A') ;
x = Q*(R'\b) ;
a good solution is found. To reduce fill-in:
p = colamd (A') ;
[Q,R] = qr (A (p,:)') ;
x = Q*(R'\b(p)) ;
which also finds a good solution.
However, x=A\b computes a basic solution, using this algorithm:
q = colamd (A) ;
[Q,R] = qr (A (:,q)) ;
x = R\(Q'*b) ;
x (q) = q ;
which finds an error with norm(A*x-b) of 1e-9 in MATLAB 7.6.
With random permutations, and determining the cond(R1) of the leading
trianglar part (R is "squeezed" and the columns can be partitioned into
[R1 R2] where R1 is square and upper triangular) leads to the following
results.
Note that the error is high when condest(R1) is high. Note in
particular the last trial.
So this clinches the question. MATLAB's QR, and my new sparse QR, both
use a rank-detection method (by Heath) that does not do column pivoting,
and which is known to fail for some problems - for which Grimes & Lewis'
method will likely succeed.
The advantage of my QR is that I now always return R as upper
trapezoidal, so if the user is concerned, he/she can easily check
condest(R(:,1:m)) if m < n.
err 7.71e-07 condest R1 2.18e+12
err 1.25e-09 condest R1 9.82e+08
err 2.47e-09 condest R1 2.46e+11
err 4.00e-09 condest R1 4.03e+09
err 9.88e-10 condest R1 4.73e+09
err 2.25e-08 condest R1 5.34e+09
err 2.00e-08 condest R1 1.04e+09
err 1.09e-09 condest R1 6.83e+08
err 6.18e-08 condest R1 8.13e+10
err 3.13e-10 condest R1 4.23e+09
err 6.64e-10 condest R1 2.46e+10
err 5.76e-09 condest R1 4.31e+09
err 7.61e-07 condest R1 5.08e+10
err 2.27e-09 condest R1 4.94e+09
err 3.99e-10 condest R1 2.80e+09
err 1.37e-09 condest R1 3.13e+09
err 6.93e-05 condest R1 1.84e+14
err 1.35e-08 condest R1 7.18e+09
err 1.09e-08 condest R1 1.79e+11
err 1.81e-09 condest R1 2.99e+08
err 1.55e-01 condest R1 2.45e+18
In summary, this is a "feature" not a "bug". If you want a reliable
solution to an underdetermined system, find the min 2norm solution
via a QR factorization of A'.
|