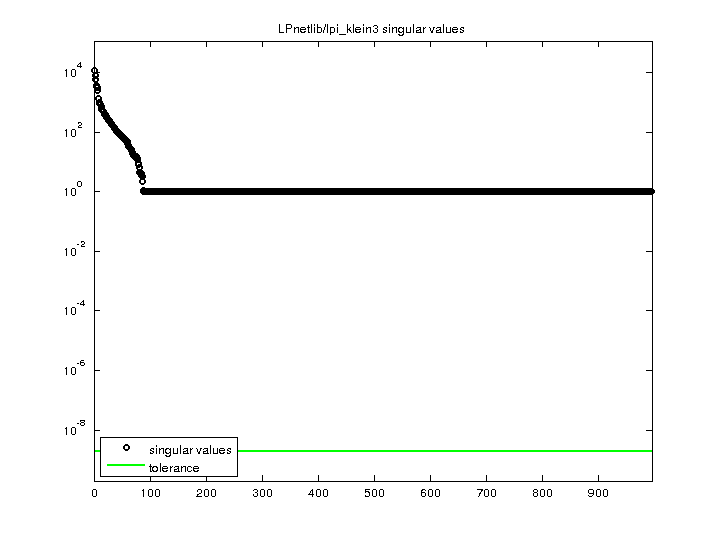
LPnetlib/lpi_klein3
Netlib LP problem klein3: minimize c'*x, where Ax=b, lo<=x<=hi
| Name |
lpi_klein3 |
| Group |
LPnetlib |
| Matrix ID |
723 |
|
Num Rows
|
994 |
|
Num Cols
|
1,082 |
|
Nonzeros
|
13,101 |
|
Pattern Entries
|
13,101 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
|
|
Author
|
E. Klotz |
|
Editor
|
J. Chinneck |
| Structural Rank |
994 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
| SVD Statistics |
| Matrix Norm |
1.142134e+04 |
| Minimum Singular Value |
1.000000e+00 |
| Condition Number |
1.142134e+04
|
| Rank |
994 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
An infeasible Netlib LP problem, in lp/infeas. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/infeas
The lp/infeas directory contains infeasible linear programming test problems
collected by John W. Chinneck, Carleton Univ, Ontario Canada. The following
are relevant excerpts from lp/infeas/readme (by John W. Chinneck):
PROBLEM DESCRIPTION
-------------------
KLEIN1, KLEIN2, KLEIN3: related small and medium size problems.
Contributor: Ed Klotz, CPLEX Optimization Inc.
Name Rows Cols Nonzeros Bounds Notes
klein3 995 88 12107
|