LPnetlib/lp_modszk1
Netlib LP problem modszk1: minimize c'*x, where Ax=b, lo<=x<=hi
| Name |
lp_modszk1 |
| Group |
LPnetlib |
| Matrix ID |
644 |
|
Num Rows
|
687 |
|
Num Cols
|
1,620 |
|
Nonzeros
|
3,168 |
|
Pattern Entries
|
3,168 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
1994 |
|
Author
|
I. Maros |
|
Editor
|
D. Gay |
| Structural Rank |
686 |
| Structural Rank Full |
false |
|
Num Dmperm Blocks
|
3 |
|
Strongly Connect Components
|
3 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
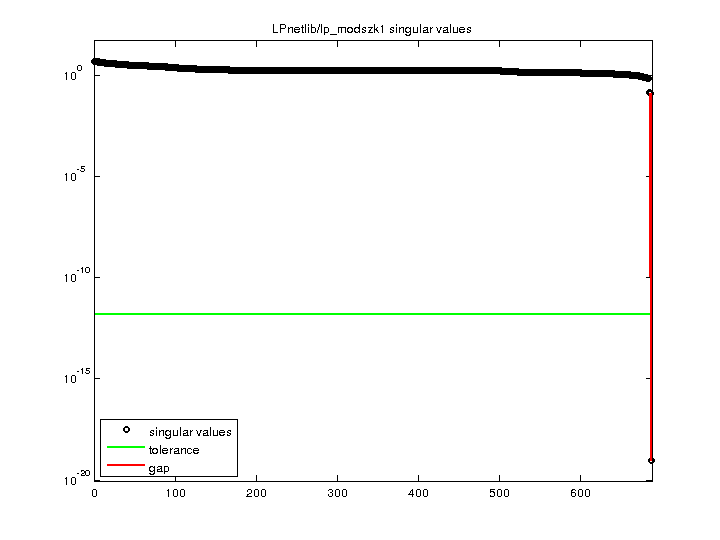
| SVD Statistics |
| Matrix Norm |
4.875560e+00 |
| Minimum Singular Value |
9.119891e-20 |
| Condition Number |
5.346073e+19
|
| Rank |
686 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
1 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
A Netlib LP problem, in lp/data. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/data
The following are relevant excerpts from lp/data/readme (by David M. Gay):
The column and nonzero counts in the PROBLEM SUMMARY TABLE below exclude
slack and surplus columns and the right-hand side vector, but include
the cost row. We have omitted other free rows and all but the first
right-hand side vector, as noted below. The byte count is for the
MPS compressed file; it includes a newline character at the end of each
line. These files start with a blank initial line intended to prevent
mail programs from discarding any of the data. The BR column indicates
whether a problem has bounds or ranges: B stands for "has bounds", R
for "has ranges". The BOUND-TYPE TABLE below shows the bound types
present in those problems that have bounds.
The optimal value is from MINOS version 5.3 (of Sept. 1988)
running on a VAX with default options.
PROBLEM SUMMARY TABLE
Name Rows Cols Nonzeros Bytes BR Optimal Value
MODSZK1 688 1620 4158 40908 B 3.2061972906E+02
BOUND-TYPE TABLE
MODSZK1 FR
From Istvan Maros.
Concerning the problems he submitted, Istvan Maros says that
MODSZK1 is a "real-life problem" that
is "very degenerate" and on which a dual simplex algorithm "may require
up to 10 times" fewer iterations than a primal simplex algorithm. It
"is a multi-sector economic planning model (a kind of an input/output
model in economy)" and "is an old problem of mine and it is not easy to
recall more."
Added to Netlib on 17 Jan. 1994
|