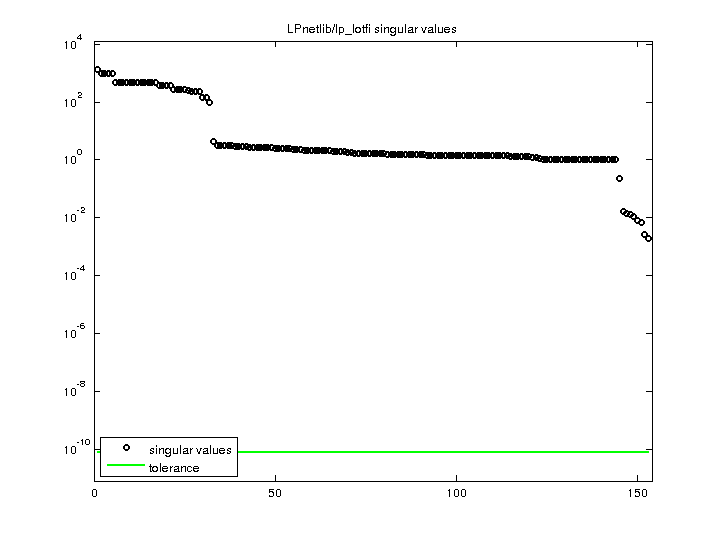
LPnetlib/lp_lotfi
Netlib LP problem lotfi: minimize c'*x, where Ax=b, lo<=x<=hi
| Name |
lp_lotfi |
| Group |
LPnetlib |
| Matrix ID |
641 |
|
Num Rows
|
153 |
|
Num Cols
|
366 |
|
Nonzeros
|
1,136 |
|
Pattern Entries
|
1,136 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
1989 |
|
Author
|
V. Lofti |
|
Editor
|
D. Gay |
| Structural Rank |
153 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
9 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
1.275023e+03 |
| Minimum Singular Value |
1.920182e-03 |
| Condition Number |
6.640116e+05
|
| Rank |
153 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
A Netlib LP problem, in lp/data. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/data
The following are relevant excerpts from lp/data/readme (by David M. Gay):
The column and nonzero counts in the PROBLEM SUMMARY TABLE below exclude
slack and surplus columns and the right-hand side vector, but include
the cost row. We have omitted other free rows and all but the first
right-hand side vector, as noted below. The byte count is for the
MPS compressed file; it includes a newline character at the end of each
line. These files start with a blank initial line intended to prevent
mail programs from discarding any of the data. The BR column indicates
whether a problem has bounds or ranges: B stands for "has bounds", R
for "has ranges".
The optimal value is from MINOS version 5.3 (of Sept. 1988)
running on a VAX with default options.
PROBLEM SUMMARY TABLE
Name Rows Cols Nonzeros Bytes BR Optimal Value
LOTFI 154 308 1086 6718 -2.5264706062E+01
From Vahid Lotfi.
When included in Netlib: cost coefficients negated.
LOTFI, says Vahid Lotfi, "involves audit staff scheduling. This problem
is semi real world and we have used it in a study, the results of which
are to appear in Decision Sciences (Fall 1990). The detailed
description of the problem is also in the paper. The problem is
actually an MOLP with seven objectives, the first is maximization and
the other six are minimization. The version that I am sending has the
aggregated objective (i.e., z1-z2-z3-z4-z5-z6-z7)."
Added to Netlib on 27 June 1989
|