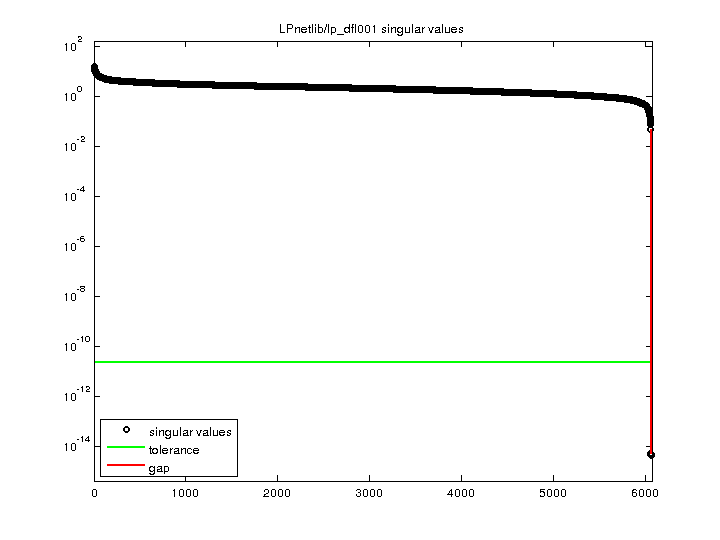
LPnetlib/lp_dfl001
Netlib LP problem dfl001: minimize c'*x, where Ax=b, lo<=x<=hi
| Name |
lp_dfl001 |
| Group |
LPnetlib |
| Matrix ID |
619 |
|
Num Rows
|
6,071 |
|
Num Cols
|
12,230 |
|
Nonzeros
|
35,632 |
|
Pattern Entries
|
35,632 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
1990 |
|
Author
|
M. Meketon |
|
Editor
|
D. Gay |
| Structural Rank |
6,071 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
1.591695e+01 |
| Minimum Singular Value |
4.036579e-15 |
| Condition Number |
3.943179e+15
|
| Rank |
6,058 |
| sprank(A)-rank(A) |
13 |
| Null Space Dimension |
13 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
A Netlib LP problem, in lp/data. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/data
The following are relevant excerpts from lp/data/readme (by David M. Gay):
The column and nonzero counts in the PROBLEM SUMMARY TABLE below exclude
slack and surplus columns and the right-hand side vector, but include
the cost row. We have omitted other free rows and all but the first
right-hand side vector, as noted below. The byte count is for the
MPS compressed file; it includes a newline character at the end of each
line. These files start with a blank initial line intended to prevent
mail programs from discarding any of the data. The BR column indicates
whether a problem has bounds or ranges: B stands for "has bounds", R
for "has ranges". The BOUND-TYPE TABLE below shows the bound types
present in those problems that have bounds.
PROBLEM SUMMARY TABLE
Name Rows Cols Nonzeros Bytes BR Optimal Value
DFL001 6072 12230 41873 353192 B 1.12664E+07 **
BOUND-TYPE TABLE
DFL001 UP
Submitted by Marc Meketon.
DFL001, says Marc Meketon, "is a 'real-world' airline schedule planning
(fleet assignment) problem. This LP was preprocessed by a modified
version of the KORBX(r) System preprocessor. The problem reduced in
size (rows, columns, non-zeros) significantly. The row and columns were
randomly sorted and renamed, and a fixed adjustment to the objective
function was eliminated. The name of the problem is derived from the
initials of the person who created it."
Bob Bixby reports that the CPLEX solver (running on a Sparc station)
finds slightly different optimal values for some of the problems.
On a MIPS processor, MINOS version 5.3 (with crash and scaling of
December 1989) also finds different optimal values for some of the
problems. The following table shows the values that differ from those
shown above. (Whether CPLEX finds different values on the recently
added problems remains to be seen.)
Problem CPLEX(Sparc) MINOS(MIPS)
DFL001 1.1266396047E+07 **
David Gay reports:
** On an IEEE-arithmetic machine (an SGI 4D/380S), I (dmg) succeeded in
getting MINOS 5.3 to report optimal objective values, 1.1261702419E+07
and 1.1249281428E+07, for DFL001 only by starting with LOAD files
derived from the solution obtained on the same machine by Bob
Vanderbei's ALPO (an interior-point code); starting from one of the
resulting "optimal" bases, MINOS ran 23914 iterations on a VAX before
reporting an optimal value of 1.1253287141E+07. When started from the
same LOAD file used on the SGI machine, MINOS on the VAX reported an
optimal value of 1.1255107696E+07. Changing the FEASIBILITY TOLERANCE
to 1.E-10 (from its default of 1.E-6) led MINOS on the SGI machine to
report "optimal" values of 1.1266408461E+07 and 1.1266402835E+07. This
clearly is a problem where the FEASIBILITY TOLERANCE, initial basis, and
floating-point arithmetic strongly affect the "optimal" solution that
MINOS reports. On the SGI machine, ALPO with SPLIT 3 found
primal: obj value = 1.126639607e+07 FEASIBLE ( 2.79e-09 )
dual: obj value = 1.126639604e+07 FEASIBLE ( 1.39e-16 )
Bob Bixby reports the following about his experience solving DFL001
with CPLEX:
First, the value for the objective function that I get running
defaults is 1.1266396047e+07, with the following residuals:
Max. unscaled (scaled) bound infeas.: 4.61853e-14 (2.30926e-14)
Max. unscaled (scaled) reduced-cost infeas.: 6.40748e-08 (6.40748e-08)
Max. unscaled (scaled) Ax-b resid.: 4.28546e-14 (4.28546e-14)
Max. unscaled (scaled) c_B-B'pi resid.: 8.00937e-08 (8.00937e-08)
The L_infinity condition number of the (scaled) optimal basis is
213737. I got exactly the same objective value solving the problem in
several different ways. I played a bit trying to get a better
reduced-cost infeasibility, but that seems hopeless (if not pointless)
given the c-Bpi residuals.
Just as an aside, this problem exhibits very interesting behavior when
solved using a simplex method. I ran reduced-cost pricing on it in
phase I, with the result that it took 465810 iterations to get
feasible. Running the default CPLEX pricing scheme, the entire
problem solved in 94337 iterations (33059 in phase I) on a
Sparcstation. Steepest-edge pricing (and a different scaling) took
25803 iterations. This is a nasty problem.
Added to Netlib on 11 Oct. 1990
9 Jan. 1991: Bixby's remarks about DFL001 added to lp/data/readme.
|