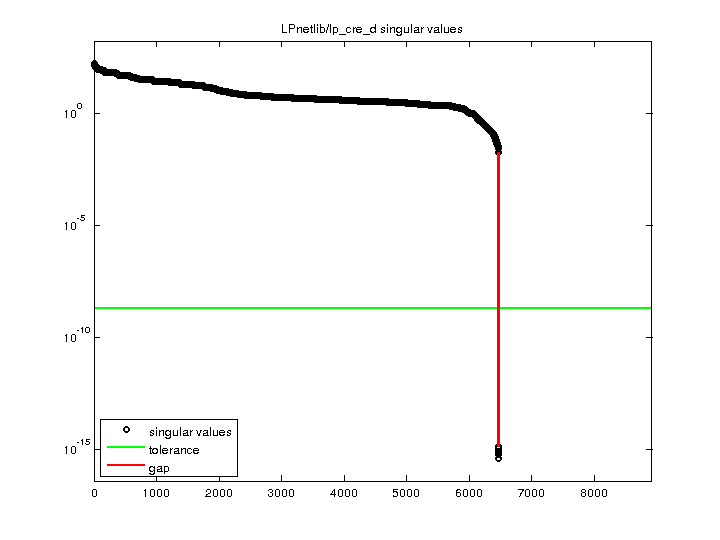
LPnetlib/lp_cre_d
Netlib LP problem cre_d: minimize c'*x, where Ax=b, lo<=x<=hi
| Name |
lp_cre_d |
| Group |
LPnetlib |
| Matrix ID |
612 |
|
Num Rows
|
8,926 |
|
Num Cols
|
73,948 |
|
Nonzeros
|
246,614 |
|
Pattern Entries
|
246,614 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
1990 |
|
Author
|
J. Kennington |
|
Editor
|
I. Lustig |
| Structural Rank |
6,476 |
| Structural Rank Full |
false |
|
Num Dmperm Blocks
|
22 |
|
Strongly Connect Components
|
2,451 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
1.813195e+02 |
| Minimum Singular Value |
0 |
| Condition Number |
Inf
|
| Rank |
6,468 |
| sprank(A)-rank(A) |
8 |
| Null Space Dimension |
2,458 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
A Netlib LP problem, in lp/data/kennington. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/data
send readme from lp/data/kennington
The following are relevant excerpts from lp/data/kennington/readme:
The "Kennington" problems: sixteen problems described in "An Empirical
Evaluation of the KORBX Algorithms for Military Airlift Applications"
by W. J. Carolan, J. E. Hill, J. L. Kennington, S. Niemi, S. J.
Wichmann (Operations Research vol. 38, no. 2 (1990), pp. 240-248).
The following table gives some statistics for the "Kennington"
problems. The number of columns excludes slacks and surpluses.
The bounds column tells how many entries appear in the BOUNDS
section of the MPS file. The mpc column shows the bytes in
the problem after "uncompress" and before "emps"; MPS shows
the bytes after "emps". The optimal values were computed by
Vanderbei's ALPO, running on an SGI computer (with binary IEEE
arithmetic).
Name rows columns nonzeros bounds mpc MPS optimal value
CRE-A 3517 4067 19054 0 152726 659682 2.3595407e+07
CRE-B 9649 72447 328542 0 2119719 10478735 2.3129640e+07
CRE-C 3069 3678 16922 0 135315 587817 2.5275116e+07
CRE-D 8927 69980 312626 0 2022105 9964196 2.4454970e+07
KEN-07 2427 3602 11981 7204 150525 718748 -6.7952044e+08
KEN-11 14695 21349 70354 42698 928171 4167698 -6.9723823e+09
KEN-13 28633 42659 139834 85318 1836457 8254122 -1.0257395e+10
KEN-18 105128 154699 512719 309398 7138893 29855000 -5.2217025e+10
OSA-07 1119 23949 167643 0 1059475 5388666 5.3572252e+05
OSA-14 2338 52460 367220 0 2359656 11800249 1.1064628e+06
OSA-30 4351 100024 700160 0 4470876 22495351 2.1421399e+06
OSA-60 10281 232966 1630758 0 10377094 52402461 4.0440725e+06
PDS-02 2954 7535 21252 2134 197821 801690 2.8857862e+10
PDS-06 9882 28655 82269 9240 769564 3124272 2.7761038e+10
PDS-10 16559 48763 140063 16148 1313834 5331274 2.6727095e+10
PDS-20 33875 105728 304153 34888 2856653 11550890 2.3821659e+10
Submitted to Netlib by Irv Lustig.
|