JGD_SL6/D_11
Differentials of the Voronoi complex of perfect forms
| Name |
D_11 |
| Group |
JGD_SL6 |
| Matrix ID |
2193 |
|
Num Rows
|
169 |
|
Num Cols
|
461 |
|
Nonzeros
|
2,952 |
|
Pattern Entries
|
2,952 |
|
Kind
|
Combinatorial Problem |
|
Symmetric
|
No |
|
Date
|
2008 |
|
Author
|
P. Elbaz-Vincent |
|
Editor
|
J.-G. Dumas |
| Structural Rank |
168 |
| Structural Rank Full |
false |
|
Num Dmperm Blocks
|
3 |
|
Strongly Connect Components
|
6 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
| SVD Statistics |
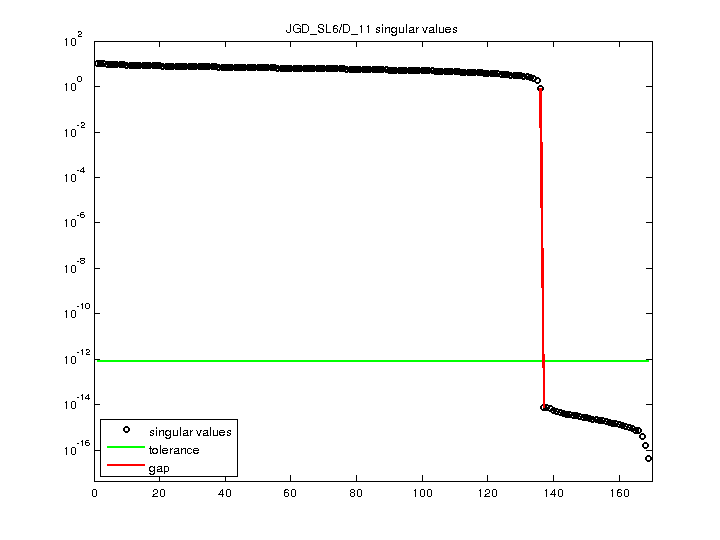
| Matrix Norm |
1.001854e+01 |
| Minimum Singular Value |
4.542673e-17 |
| Condition Number |
2.205429e+17
|
| Rank |
136 |
| sprank(A)-rank(A) |
32 |
| Null Space Dimension |
33 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Differentials of the Voronoi complex of perfect forms
from Philippe Elbaz-Vincent, Institut Fourier, Grenoble, France.
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html
http://www-fourier.ujf-grenoble.fr/-Informations-personnelles-.html?P=pev
D_5 Smith Invariants = [ 1:92 3:2 18:1 ]
D_6 Smith Invariants = [ 1:338 2:1 ]
D_7 Smith Invariants = [ 1:621 2:5 6:1 60:2 ]
D_8 Smith Invariants = [ 1:637 3:3 12:1 ]
D_9 Smith Invariants = [ 1:491 ]
D_10 Smith Invariants = [ 1:318 2:3 4:2 ]
D_11 Smith Invariants = [ 1:129 2:6 6:1 ]
Filename in JGD collection: SL6/D_11.sms
|