JGD_Margulies/kneser_8_3_1
Combinatorial optimization as polynomial eqns, Susan Margulies, UC Davis
| Name |
kneser_8_3_1 |
| Group |
JGD_Margulies |
| Matrix ID |
2165 |
|
Num Rows
|
15,737 |
|
Num Cols
|
15,681 |
|
Nonzeros
|
47,042 |
|
Pattern Entries
|
47,042 |
|
Kind
|
Combinatorial Problem |
|
Symmetric
|
No |
|
Date
|
2008 |
|
Author
|
S. Margulies |
|
Editor
|
J.-G. Dumas |
| Structural Rank |
14,897 |
| Structural Rank Full |
false |
|
Num Dmperm Blocks
|
3 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
binary |
| SVD Statistics |
| Matrix Norm |
4.773574e+00 |
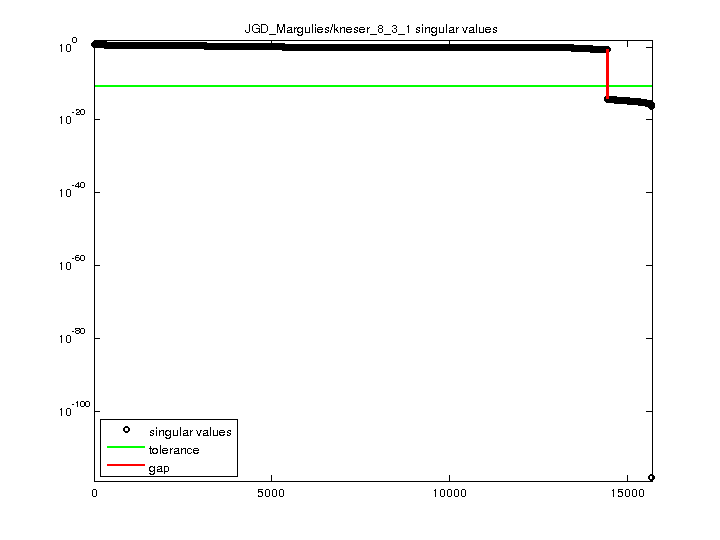
| Minimum Singular Value |
7.455411e-119 |
| Condition Number |
6.402831e+118
|
| Rank |
14,421 |
| sprank(A)-rank(A) |
476 |
| Null Space Dimension |
1,260 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Combinatorial optimization as polynomial eqns, Susan Margulies, UC Davis
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html
http://arxiv.org/abs/0706.0578
Expressing Combinatorial Optimization Problems by Systems of Polynomial
Equations and the Nullstellensatz
Authors: J.A. De Loera, J. Lee, Susan Margulies, S. Onn
(Submitted on 5 Jun 2007)
Abstract: Systems of polynomial equations over the complex or real
numbers can be used to model combinatorial problems. In this way, a
combinatorial problem is feasible (e.g. a graph is 3-colorable,
hamiltonian, etc.) if and only if a related system of polynomial
equations has a solution. In the first part of this paper, we construct
new polynomial encodings for the problems of finding in a graph its
longest cycle, the largest planar subgraph, the edge-chromatic number,
or the largest k-colorable subgraph. For an infeasible polynomial
system, the (complex) Hilbert Nullstellensatz gives a certificate that
the associated combinatorial problem is infeasible. Thus, unless P =
NP, there must exist an infinite sequence of infeasible instances of
each hard combinatorial problem for which the minimum degree of a
Hilbert Nullstellensatz certificate of the associated polynomial system
grows. We show that the minimum-degree of a Nullstellensatz
certificate for the non-existence of a stable set of size greater than
the stability number of the graph is the stability number of the graph.
Moreover, such a certificate contains at least one term per stable set
of G. In contrast, for non-3- colorability, we found only graphs with
Nullstellensatz certificates of degree four.
Filename in JGD collection: Margulies/kneser_8_3_1.sms
|