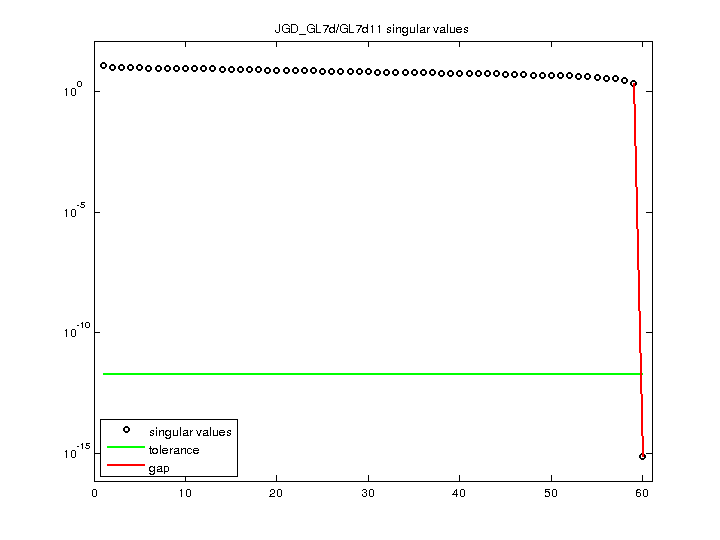
JGD_GL7d/GL7d11
Differentials of the Voronoi complex of perfect forms of rank 7 mod GL_7(Z)
| Name |
GL7d11 |
| Group |
JGD_GL7d |
| Matrix ID |
1984 |
|
Num Rows
|
1,019 |
|
Num Cols
|
60 |
|
Nonzeros
|
1,513 |
|
Pattern Entries
|
1,513 |
|
Kind
|
Combinatorial Problem |
|
Symmetric
|
No |
|
Date
|
2008 |
|
Author
|
P. Elbaz-Vincent |
|
Editor
|
J.-G. Dumas |
| Structural Rank |
60 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
238 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
| SVD Statistics |
| Matrix Norm |
1.213100e+01 |
| Minimum Singular Value |
7.368600e-16 |
| Condition Number |
1.646310e+16
|
| Rank |
59 |
| sprank(A)-rank(A) |
1 |
| Null Space Dimension |
1 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Differentials of the Voronoi complex of perfect forms of rank 7 mod GL_7(Z)
equivalences, (related to the cohomology of GL_7(Z) and the K-theory of Z).
from Philippe Elbaz-Vincent, Institut Fourier, Grenoble, France.
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html
http://www-fourier.ujf-grenoble.fr/-Informations-personnelles-.html?P=pev
mtx rank n m ker rank/min(n,m) homology
10 1 60 1 59
11 59 1019 60 960 0,98333 0
12 960 8899 1019 7939 0,94210 1
13 7938 47271 8899 39333 0,89201 1
14 39332 171375 47271 132043 0,83205 0
15 132043 460261 171375 328218 0,77049 0
16 328218 955128 460261 626910 0,71311 0
17 626910 1548650 955128 921740 0,65636 0*
18 921740* 1955309 1548650 1033569* 0,60* 1/0*
19 103356(8/9)* 1911130 1955309 87756(2/1)* 0,54* 0/1*
20 877562 1437547 1911130 559985 0,61 0
21 559985 822922 1437547 262937 0,68048 0
22 262937 349443 822922 86506 0,75245 0
23 86505 105054 349443 18549 0,82343 1
24 18549 21074 105054 2525 0,88018 0
25 2525 2798 21074 273 0,90243 0
26 273 305 2798 32 0,89508 0
file size elements rank SF
GL7d10 1 x 60 8 1 1 (1)
GL7d11 60 x 1019 1513 59 1 (59)
GL7d12 1019 x 8899 37519 960 1 (958), 2 (2)
GL7d13 8899 x 47271 356232 7938 1 (7937), 2 (1)
GL7d14 47271 x 171375 1831183 39332 1 (39300),2 (29),4 (3)
GL7d15 171375 x 460261 6080381 132043 1 (131993), 2*??? (46), 6*??? (4)
GL7d16 955128 x 460261 14488881 328218
GL7d17 1548650 x 955128 25978098
GL7d18 1955309 x 1548650 35590540
GL7d19 1911130 x 1955309 37322725
GL7d20 1437547 x 1911130 29893084 877562
GL7d21 822922 x 1437547 18174775 559985
GL7d22 349443 x 822922 8251000 262937
GL7d23 105054 x 349443 2695430 86505 1 (86488), 2*??? (12), 6*??? (5)
GL7d24 21074 x 105054 593892 18549 1 (18544),2 (4),4 (1)
GL7d25 21074 x 2798 81671 2525 1 (2507), 2 (18)
GL7d26 2798 x 305 7412 273 1 (258), 2 (7), 6 (7), 36 (1)
Filename in JGD collection: GL7d/GL7d11.sms
|