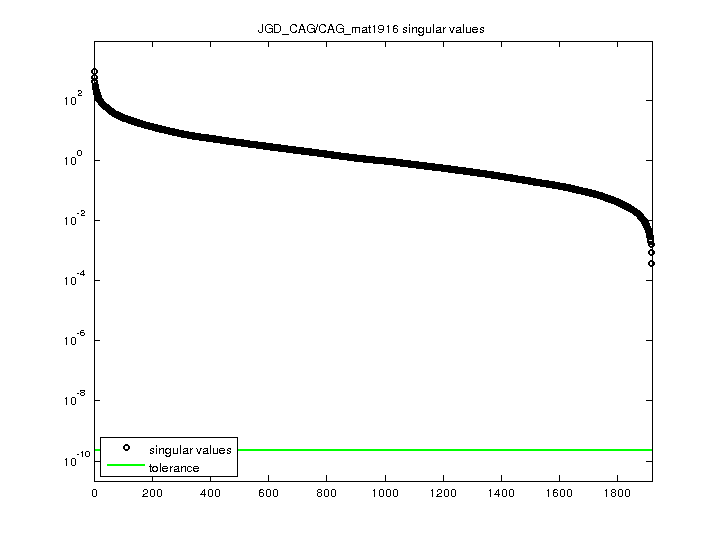
JGD_CAG/CAG_mat1916
CAG matrix set from Michael Monagan, Simon Fraser Univ., Canada
| Name |
CAG_mat1916 |
| Group |
JGD_CAG |
| Matrix ID |
1941 |
|
Num Rows
|
1,916 |
|
Num Cols
|
1,916 |
|
Nonzeros
|
195,985 |
|
Pattern Entries
|
195,985 |
|
Kind
|
Combinatorial Problem |
|
Symmetric
|
No |
|
Date
|
2008 |
|
Author
|
M. Monagan |
|
Editor
|
J.-G. Dumas |
| Structural Rank |
1,916 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
31 |
|
Strongly Connect Components
|
31 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
30% |
|
Numeric Symmetry
|
21.2% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
| SVD Statistics |
| Matrix Norm |
9.171274e+02 |
| Minimum Singular Value |
3.761160e-04 |
| Condition Number |
2.438416e+06
|
| Rank |
1,916 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
CAG matrix set from Michael Monagan, Simon Fraser Univ., Canada
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html
Strongly Connected Graph Components and Computing
Characteristic Polynomials of Integer Matrices in Maple,
Simon Lo, Michael Monagan, Allan Wittkopf
{sclo,mmonagan,wittkopf} at cecm.sfu.ca
Centre for Experimental and Constructive Mathematics,
Department of Mathematics, Simon Fraser University,
Burnaby, B.C., V5A 1S6, Canada.
abstract:
Let A be an n x n matrix of integers. We present details of our Maple
implementation of a simple modular method for computing the
characteristic polynomial of A. We consider several different
representations for the computation modulo primes, in particular, the
use of double precision floats. The algorithm used in Maple releases
7-10 is the Berkowitz algorithm. We present some timings comparing the
two algorithms on a sequence of matrices arising from an application in
combinatorics of Jocelyn Quaintance. These matrices have a hidden block
structure. Once identified, we can further reduce the computing time
dramatically. This work has been incorporated into Maple 11's
LinearAlgebra package.
http://www.cecm.sfu.ca/~monaganm/papers/CP8.pdf
Filename in JGD collection: CAG/mat1916.sms
|