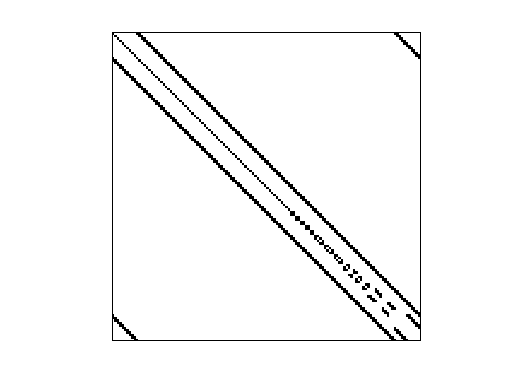
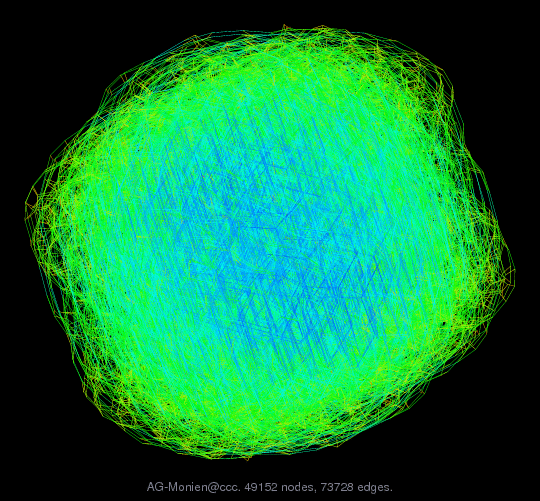
AG-Monien/ccc
cube-connected cycle graph sequence
| Name |
ccc |
| Group |
AG-Monien |
| Matrix ID |
2438 |
|
Num Rows
|
49,152 |
|
Num Cols
|
49,152 |
|
Nonzeros
|
147,456 |
|
Pattern Entries
|
147,456 |
|
Kind
|
Undirected Graph Sequence |
|
Symmetric
|
Yes |
|
Date
|
1998 |
|
Author
|
R. Diekmann, R. Preis |
|
Editor
|
R. Diekmann, R. Preis |
| Structural Rank |
|
| Structural Rank Full |
|
|
Num Dmperm Blocks
|
|
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
100% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
binary |
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
AG-Monien Graph Collection, Ralf Diekmann and Robert Preis
http://www2.cs.uni-paderborn.de/fachbereich/AG/monien/RESEARCH/PART/graphs.html
A collection of test graphs from various sources. Many of the graphs
include XY or XYZ coordinates. This set also includes some graphs from
the Harwell-Boeing collection, the NASA matrices, and some random matrices
which are not included here in the AG-Monien/ group of the UF Collection.
In addition, two graphs already appear in other groups:
AG-Monien/big : same as Nasa/barth5, Pothen/barth5 (not included here)
AG-Monien/cage_3_11 : same as Pajek/GD98_c (included here)
The AG-Monien/GRID subset is not included. It contains square grids that
are already well-represented in the UF Collection.
Six of the problem sets are included as sequences, each sequence being
a single problem instance in the UF Collection:
bfly: 10 butterfly graphs 3..12
cage: 45 cage graphs 3..12
cca: 10 cube-connected cycle graphs, no wrap
ccc: 10 cube-connected cycle graphs, with wrap
debr: 18 De Bruijn graphs
se: 13 shuffle-exchange graphs
Problem.aux.G{:} are the graphs in these 6 sequences. Problem.aux.Gname{:}
are the original names of each graph, and Problemm.aux.Gcoord{:} are the
xy or xyz coordinates of each node, if present.
Graphs in the ccc sequence:
1 : CCC3 : 24 nodes 36 edges 72 nonzeros
2 : CCC4 : 64 nodes 96 edges 192 nonzeros
3 : CCC5 : 160 nodes 240 edges 480 nonzeros
4 : CCC6 : 384 nodes 576 edges 1152 nonzeros
5 : CCC7 : 896 nodes 1344 edges 2688 nonzeros
6 : CCC8 : 2048 nodes 3072 edges 6144 nonzeros
7 : CCC9 : 4608 nodes 6912 edges 13824 nonzeros
8 : CCC10 : 10240 nodes 15360 edges 30720 nonzeros
9 : CCC11 : 22528 nodes 33792 edges 67584 nonzeros
10 : CCC12 : 49152 nodes 73728 edges 147456 nonzeros
The primary graph (Problem.A) in this sequence is the last graph
in the sequence.
|