LPnetlib/lpi_vol1
Netlib LP problem vol1: minimize c'*x, where Ax=b, lo<=x<=hi
| Name |
lpi_vol1 |
| Group |
LPnetlib |
| Matrix ID |
730 |
|
Num Rows
|
323 |
|
Num Cols
|
464 |
|
Nonzeros
|
1,646 |
|
Pattern Entries
|
1,646 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
1993 |
|
Author
|
T. Baker |
|
Editor
|
J. Chinneck |
| Structural Rank |
323 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
13 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
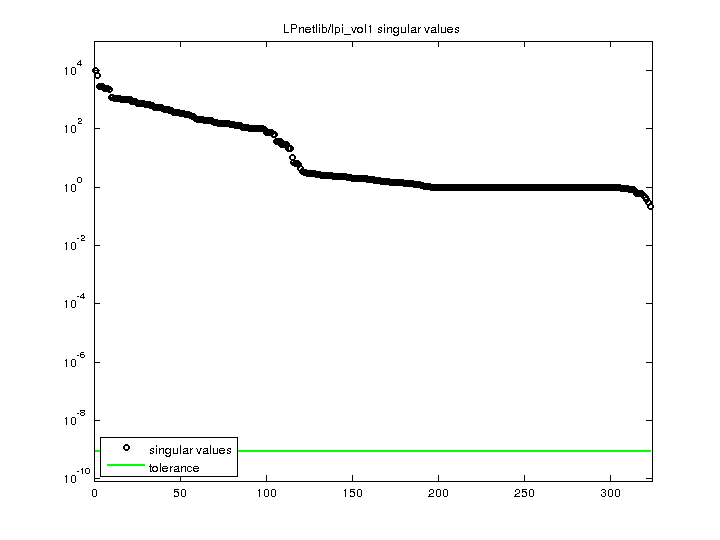
1.011726e+04 |
| Minimum Singular Value |
2.096247e-01 |
| Condition Number |
4.826369e+04
|
| Rank |
323 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
An infeasible Netlib LP problem, in lp/infeas. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/infeas
The lp/infeas directory contains infeasible linear programming test problems
collected by John W. Chinneck, Carleton Univ, Ontario Canada. The following
are relevant excerpts from lp/infeas/readme (by John W. Chinneck):
In the following, IIS stands for Irreducible Infeasible Subsystem, a set
of constraints which is itself infeasible, but becomes feasible when any
one member is removed. Isolating an IIS from within the larger set of
constraints defining the model is one analysis approach.
PROBLEM DESCRIPTION
-------------------
CHEMCOM, QUAL, REFINERY, REACTOR, VOL1: medium size problems derived
from a petrochemical plant model. Doctored to generate infeasibility
due to inability to meet volume or quality restrictions. With the
exception of REACTOR, these are highly volatile problems, yielding IISs
of varying sizes when different IIS isolation algorithms are applied.
See Chinneck [1993] for further discussion. Contributor: Tom Baker,
Chesapeake Decision Sciences.
Name Rows Cols Nonzeros Bounds Notes
vol1 324 464 1714 B FX
REFERENCES
----------
J.W. Chinneck (1993). "Finding the Most Useful Subset of Constraints
for Analysis in an Infeasible Linear Program", technical report
SCE-93-07, Systems and Computer Engineering, Carleton University,
Ottawa, Canada.
|