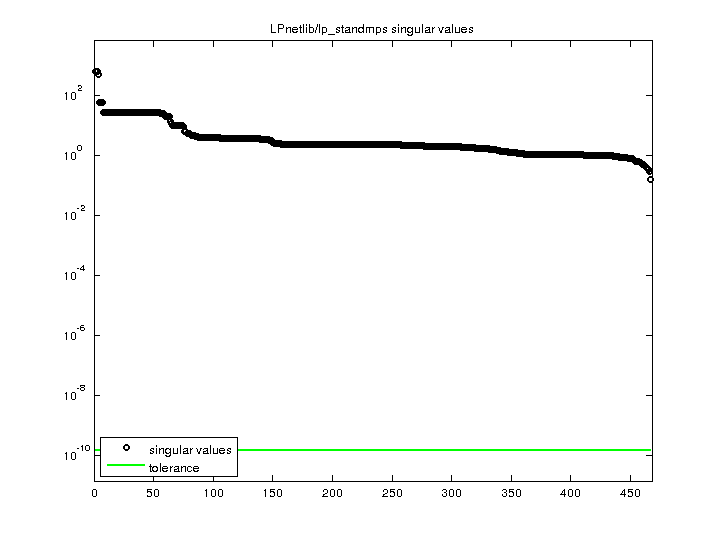
LPnetlib/lp_standmps
Netlib LP problem standmps: minimize c'*x, where Ax=b, lo<=x<=hi
| Name |
lp_standmps |
| Group |
LPnetlib |
| Matrix ID |
694 |
|
Num Rows
|
467 |
|
Num Cols
|
1,274 |
|
Nonzeros
|
3,878 |
|
Pattern Entries
|
3,878 |
|
Kind
|
Linear Programming Problem |
|
Symmetric
|
No |
|
Date
|
1989 |
|
Author
|
R. Fourer |
|
Editor
|
R. Fourer |
| Structural Rank |
467 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
6.713151e+02 |
| Minimum Singular Value |
1.617466e-01 |
| Condition Number |
4.150412e+03
|
| Rank |
467 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
A Netlib LP problem, in lp/data. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/data
The following are relevant excerpts from lp/data/readme (by David M. Gay):
The column and nonzero counts in the PROBLEM SUMMARY TABLE below exclude
slack and surplus columns and the right-hand side vector, but include
the cost row. We have omitted other free rows and all but the first
right-hand side vector, as noted below. The byte count is for the
MPS compressed file; it includes a newline character at the end of each
line. These files start with a blank initial line intended to prevent
mail programs from discarding any of the data. The BR column indicates
whether a problem has bounds or ranges: B stands for "has bounds", R
for "has ranges". The BOUND-TYPE TABLE below shows the bound types
present in those problems that have bounds.
The optimal value is from MINOS version 5.3 (of Sept. 1988)
running on a VAX with default options.
PROBLEM SUMMARY TABLE
Name Rows Cols Nonzeros Bytes BR Optimal Value
STANDMPS 468 1075 3686 29839 B 1.4060175000E+03
BOUND-TYPE TABLE
STANDMPS UP FX
Supplied by Bob Fourer.
STANDGUB includes GUB markers; with these lines removed (lines in
the expanded MPS file that contain primes, i.e., that mention the rows
'EGROUP' and 'ENDX'), STANDGUB becomes the same as problem STANDATA;
MINOS does not understand the GUB markers, so we cannot report an
optimal value from MINOS for STANDGUB. STANDMPS amounts to STANDGUB
with the GUB constraints as explicit constraints.
Source: consulting.
|