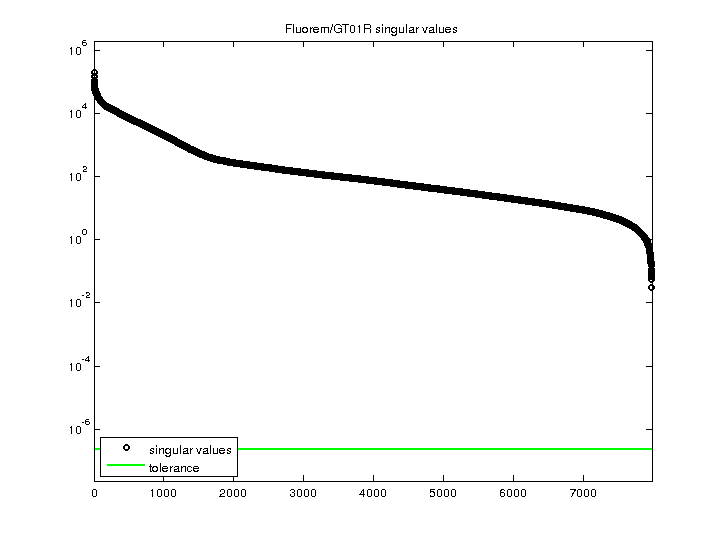
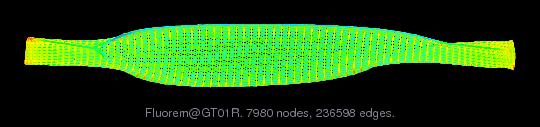
Fluorem/GT01R
GT01R: 2D inviscid case. F. Pacull, Lyon, France
| Name |
GT01R |
| Group |
Fluorem |
| Matrix ID |
2335 |
|
Num Rows
|
7,980 |
|
Num Cols
|
7,980 |
|
Nonzeros
|
430,909 |
|
Pattern Entries
|
430,909 |
|
Kind
|
Computational Fluid Dynamics Problem |
|
Symmetric
|
No |
|
Date
|
2010 |
|
Author
|
F. Pacull |
|
Editor
|
T. Davis |
| Structural Rank |
7,980 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
4 |
|
Strongly Connect Components
|
4 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
88.1% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
1.950065e+05 |
| Minimum Singular Value |
3.086683e-02 |
| Condition Number |
6.317673e+06
|
| Rank |
7,980 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
CFD matrices from Francois Pacull, FLUOREM, in Lyon, France
We are dealing with CFD and more precisely steady flow
parametrization. The equations involved are the compressible
Navier-Stokes ones (RANS). These matrices are real, square and
indefinite, they correspond to the Jacobian with respect the
conservative fluid variables of the discretized governing
equations (finite-volume discretization). Thus they have a
block structure (corresponding to the mesh nodes: the block
size is the number of variables per mesh node), they are not
symmetric (however, their blockwise structure has a high level
of symmetry) and they often show some kind of hyperbolic
behavior. They have not been scaled or reordered.
They are generated through automatic differentiation of the
flow solver around a steady state. A right hand-side is also
given for each matrix: this represents the derivative of the
equations with respect to a parameter (of operation or shape).
Since they are generated automatically, they may have "silent"
variables: these are variables corresponding to an identity
submatrix associated with a null right hand-side, for example
one of the three velocity components in a 2D case, or the
turbulent variables in a "frozen" turbulence case.
We believe that these matrices are good test cases when
studying preconditioning methods for iterative methods, such as
block incomplete factorization, or when studying domain
decomposition methods or deflation. They are actually being
studied by a few researchers in France regarding numerical
methods, through the LIBRAERO research project of the ANR (national
research agency): ANR-07-TLOG-011.
Francois Pacull, Lyon, France. fpacull at fluorem.com
Specific problem descriptions:
GT01R: 2D inviscid case
number of mesh nodes: 1596
block size: 5
variables: [rho,rho*u,rho*v,rho*w,rho*E]
(rho w is "silent", the fourth row and column in each
block can be removed)
matrix order: 7980
nnz: 430909
comments: This is a 2D linear cascade turbine case. The grid
corresponds to one inter-blade channel. The stencil involved
by the convective scheme uses 9 nodes. Thus, there are 9
non-zero blocks for each node in the matrix. The specificity
is that the computational domain is periodic, which introduces
some non-zeros elements far away from the diagonal.
|